Pricing Options with the Black-Scholes Model [Short]
Recently, I have been learning about optimal options pricing under various sets of assumptions. The introduction to risk-neutral options pricing is the Black-Scholes model, which assumes you have an arbitrage free market with at least one risk-free asset and one risky asset. Additionally you assume that the log-price of the risky asset follows a Wiener process. i.e. Geometric Brownian motion.
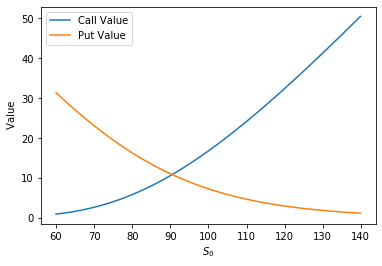
When a perfectly good source exists there is no purpose for me to fully repeat the information. See codearmo for an implementation of options pricing under the Black-Scholes Model in Python.
Motivations
I am motivated to learn about options pricing because I believe that the stock/derivative markets offer ample opportunity to learn about statistics in a often adversarial environment. Additionally, I wanted some project to get used to writing notes in Obsidian for.
Resources I used for learning about options pricing
Contributors to Wikimedia projects
Full Bio/BlackScholesMerton-56a6d22e3df78cf772906866.png)
Contributors to Wikimedia projects
Contributors to Wikimedia projects